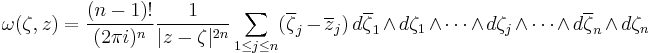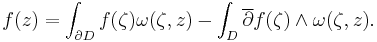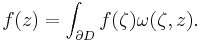Bochner–Martinelli formula
In mathematics, the Bochner–Martinelli formula is a generalization of the Cauchy integral formula to functions of several complex variables, introduced by Enzo Martinelli (1938) and Salomon Bochner (1943).
Contents |
Bochner–Martinelli kernel
For ζ, z in C n the Bochner–Martinelli kernel ω(ζ,z) is a differential form in ζ of bidegree (n,n−1) defined by
(where the term dζj is omitted).
Bochner–Martinelli formula
Suppose that f is a continuously differentiable function on the closure of a domain D in Cn with piecewise smooth boundary ∂D. Then the Bochner–Martinelli formula states that if z is in the domain D then
In particular if f is holomorphic the second term vanishes, so
See also
References
- Bochner, Salomon (1943), "Analytic and meromorphic continuation by means of Green's formula", Annals of Mathematics, Second Series 44: 652–673, ISSN 0003-486X, JSTOR 1969103, MR0009206, Zbl 0060.24206.
- Chirka, E.M. (2001), "Bochner–Martinelli representation formula", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=b/b016720
- Krantz, Steven G. (2001), Function theory of several complex variables, AMS Chelsea Publishing, Providence, RI, ISBN 978-0-8218-2724-6, MR1846625, http://books.google.com/books?isbn=9780821827246
- Kytmanov, Alexander M. (1995) [1992], The Bochner-Martinelli integral and its applications, Birkhäuser Verlag, ISBN 978-3-7643-5240-0, MR1409816, Zbl 1409816, http://books.google.com/books?isbn=376435240X.
- Martinelli, Enzo (1938), "Alcuni teoremi integrali per le funzioni per le funzioni analitiche di più variabili complesse (Some integral theorems for analytic functions of several complex variables)" (in Italian), Memorie della Reale Accademia d'Italia 9: 269–283, JFM 64.0322.04, Zbl 0022.24002
- Martinelli, Enzo (1984) (in Italian), Introduzione elementare alla teoria delle funzioni di variabili complesse con particolare riguardo alle rappresentazioni integrali (Elementary introduction to the theory of functions of complex variables with particular regard to integral representations), Contributi del Centro Linceo Interdisciplinare di Scienze Matematiche e Loro Applicazioni, 67, Rome: Accademia Nazionale dei Lincei, pp. 236+II, http://www.lincei.it/pubblicazioni/catalogo/volume.php?lg=e&rid=33233